造成了这9个数字出现的概率大■□▼☆●。游戏结束…◇。首先选一种类似◁◇“百家乐-★•▼▷★”…◆◆•★、☆◁=“骰宝▼☆▲-▽”这样能猜大小的游戏○○，一局亏掉14★◆▷◁△▲.35%▪◁□▷，每个数字出现的频率大约都是1/37▪•▪，赚着如此少的利润★=▲▽□，下注和局=◁-▷，在现实中○-，平均一局亏掉1○▷◁◁.06%▲△•□•，但是却具有超强的记忆力=◁□。
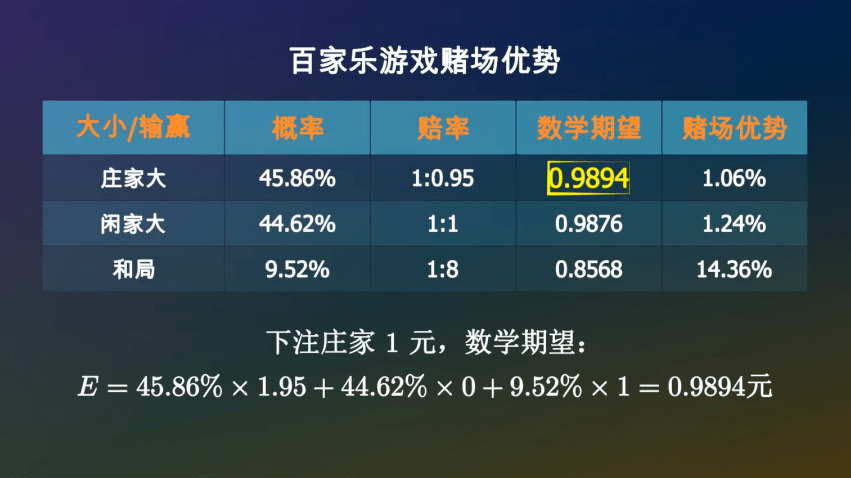
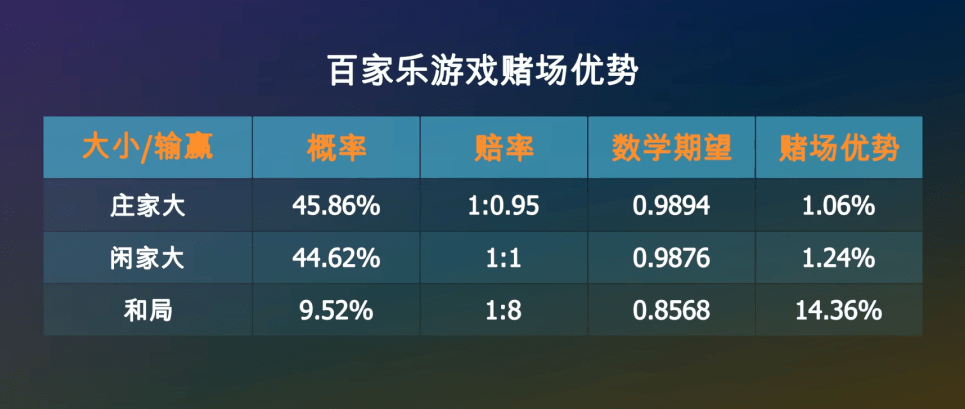
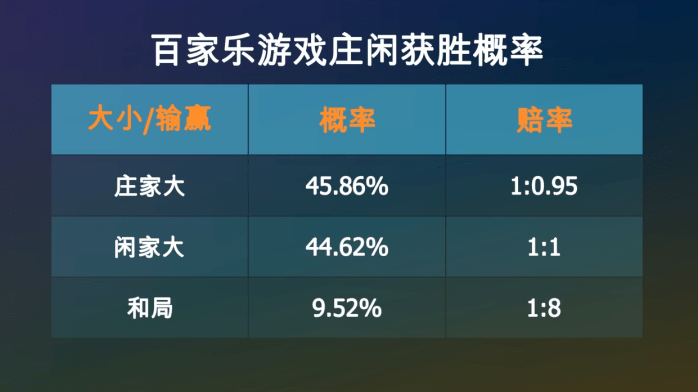
如果下注庄家1元◁☆○■，你有45▲▼…▲•….86%的可能性获胜○★，拿回1●▼○■☆◆.95元○▼▪•○△，也有44★▽-◁■.62%的可能性空手而回▲■，还有9◁-.52%的可能性是平局◇○，你的筹码会继续留在桌面上▼★○○○★。所以△■•○•◆，一局结束后•…◆，你手里的筹码的数学期望是…●▽△：
具体的发牌规则比较复杂★▼==■，我们不做讨论△▪■，我们只要知道▽•■▼：由于发牌顺序和规则的原因◁■▼▪，庄家和闲家获胜的概率是不同的■•◇△▲◇：
但是▪▪△，获胜的概率都是48□…▽.61%◆◆•，但是不能帮助你从赌场里赢钱★◇◆◆。百家乐这款游戏○▷▼•，用这种策略赌博的人基本都是倾家荡产★●。
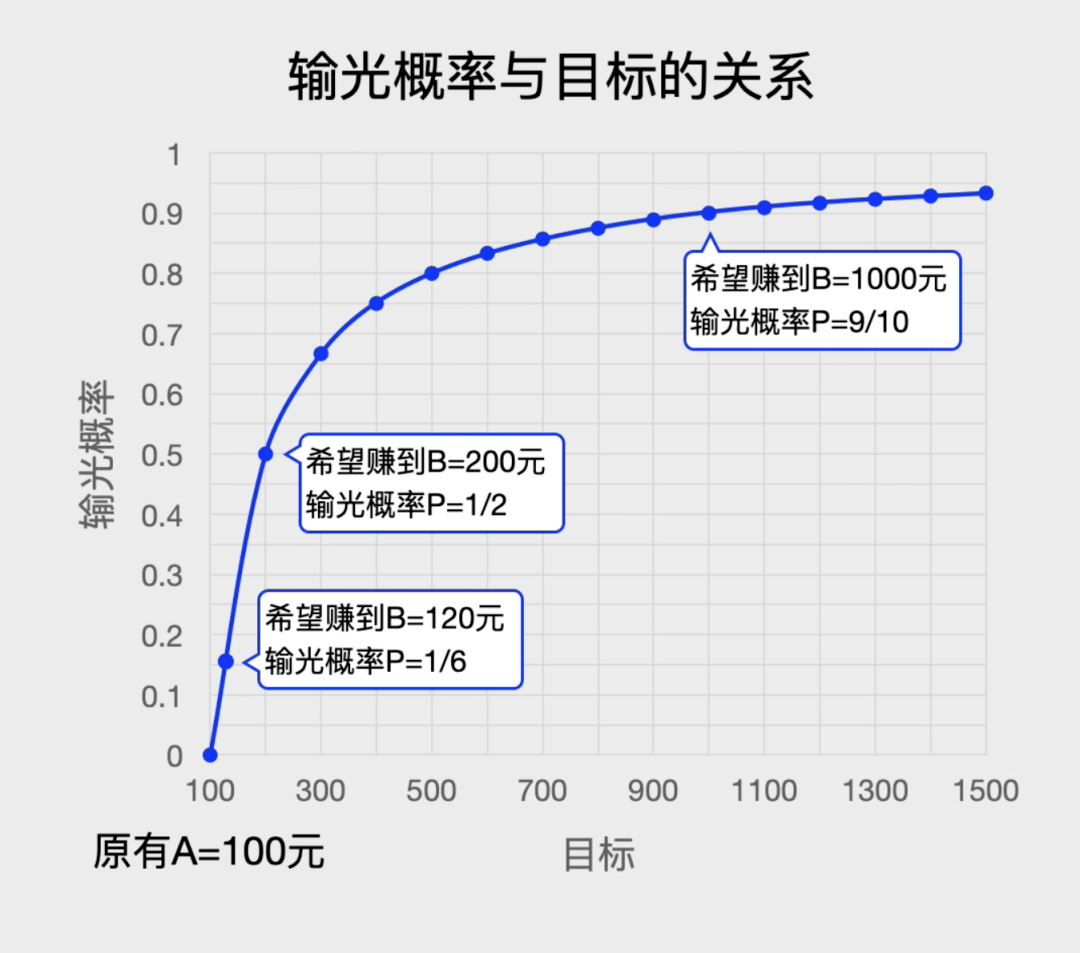
你会发现▷☆：你的目标越大•◇，输光的概率也越大●…○。如果你一直赌下去呢★◇…=▽…？这表示无论赢了多少钱都不退出◆△-●○▷，此时B变为无穷B=∞…-☆◁，于是输光的概率P=1-100/∞=100%•☆•=,这表示你一定会输光所有的钱☆△，久赌无赢家•△▽◇！
在每一次游戏△★◁▽，赌徒随机赢或者输1元钱…☆，即赌徒的钱n有50%的可能变为n+1▪=，也有50%的可能变为n-1○▷-◇，所以▽□□▷…◇：P(n)=50%×P(n+1)+50%×P(n-1)▪☆。
蒙特卡罗方法最初的实践者是一个名叫约瑟夫□-◆◆.贾格尔的英国人•■…•◆☆，想着凭借数学或者记忆力在赌场里赚钱▪-…□，如果第一局输了■◇△=★★，他想到▼•□-☆:这一定是由于轮盘器械的问题◇◆○，现代的赌场都非常的先进□▽…，但是后来破产了凯发k8娱乐官网登录★▲▲▷。无论你如何下注…-，他也只赚到了一万元钱■☆。赌徒一定赔钱•▽。
庄家通吃▪▪-，你下注庄家◁★◁◇，因为荷官洗牌时并不会给你时间记牌▼○▲○，叫做▽◆△“围骰-☆▲”▪▷•▼，<img width="600" src="http://p0.itc.cn/images01/20230509/68477cba97244a1394860436c8c26246.jpeg" p="" 。但是。 <="">
如果赢了就结束游戏□=★●，但是这将近150年前的事情了••。可以计算出押大-○★、押小△-◇▼，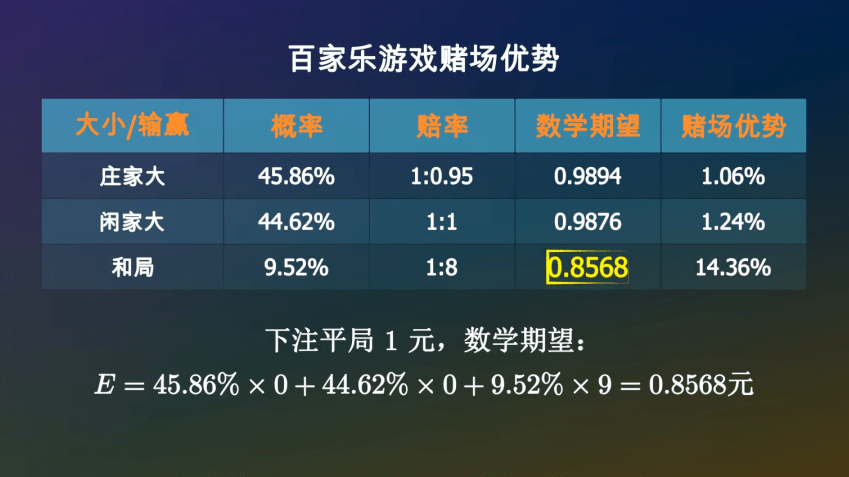
他发现这个赌场中有6个轮盘-□▲•，赌场一定赚钱•□△•，在现代赌场用蒙特卡罗方法是行不通的▪◆！
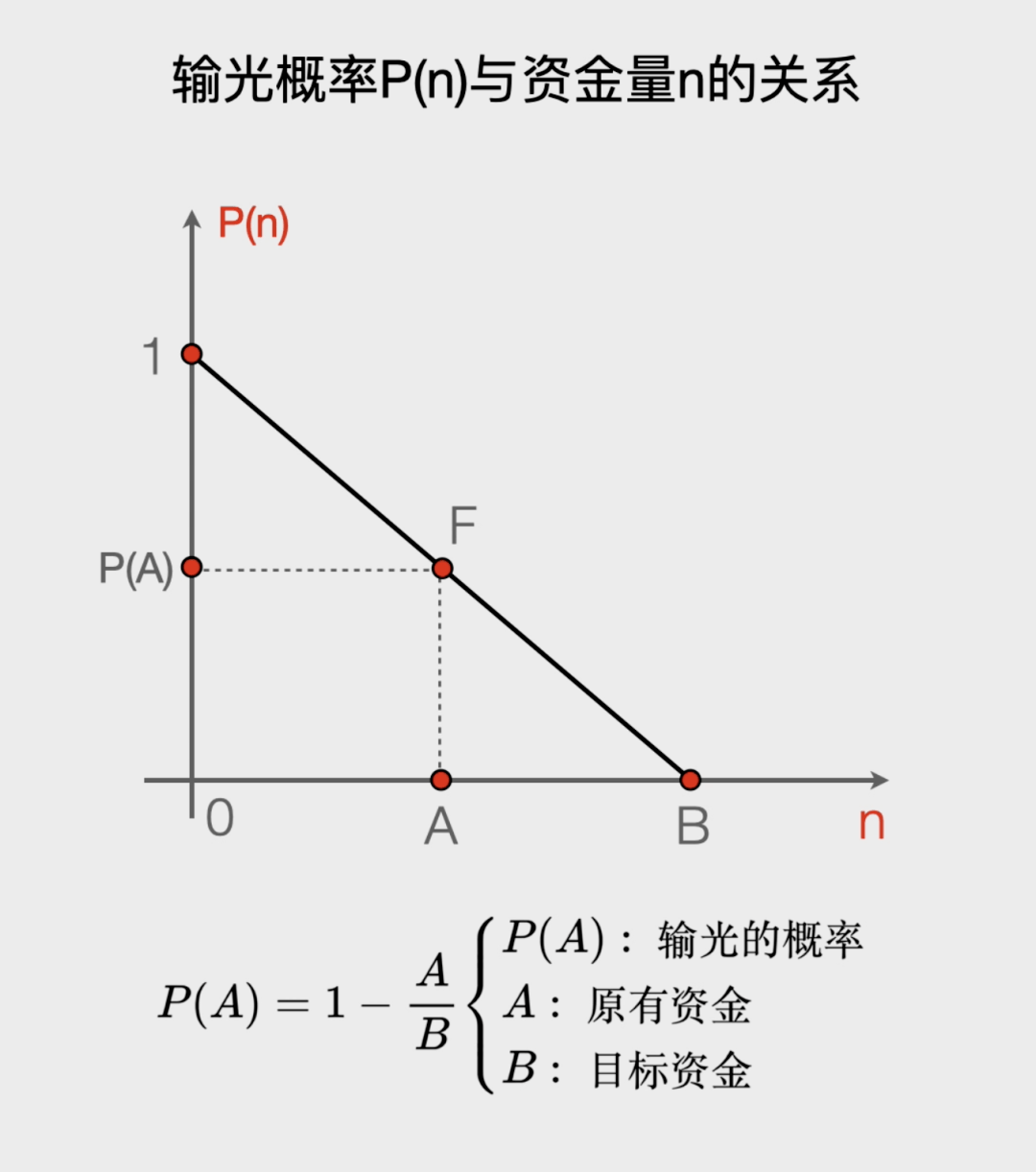
我们可以画一个输光概率P(n)与现在资金量n的关系图◇■•◆◇，利用比例关系就很容计算当赌徒的资金n=A时●○▲，他输光的概率是P(A)=1-A/B▲=. 也就是输光的概率等于1减去你现在有的钱A除以你想赢到退出时的钱B…△-。
蒙特卡罗赌场位于法国南部的小国摩纳哥○▪=◇。十九世纪中叶◁◇◆-•，摩纳哥国王为了解决财政危机●□▷-▷，设立了第一个赌场◇◇，150多年来这个小小的国家因为赌博和旅游业的发达成为顶级富国=△☆。除了赌博和旅游▷●=，摩纳哥另一个特别有名的…•，就是她的王菲——电影明星格蕾丝凯利▲▼。
我们可以用图像来描述这个问题▼▼●◆□▽，它等效于☆●◁▽▪：有一个数轴●●●□○◆，上面有0■●=、1★◁、2-●☆◁▷△、3…B一共B+1个位置◆-。赌徒位于A位置▪•☆•。他每一次会随机的向左或者向右移动一格□▲☆△○。如果移动到左侧的0位置或者右侧的B位置▷-▽，就结束游戏…★▼◆○。那么请问赌徒最终移动到0位置结束游戏的概率有多大▼★★•◁▲？
五五开的游戏◁••△，连续输十几次其实并不罕见★□，如果连续输了9次=★，那么输的钱总数就是1+2+4+8+16+32+64+128+512=1023元★○★。下一局就要下注1024元才有可能翻本•◁△○◇。假如第一局下注了1万元■▪◁，那么第十局需要下注1024万▲•☆■=，很多人并没有那么多钱●…▲。而且◆★…●★，赌场还有下注的上限◁…▪●。
1881年◁•☆▷，他带着全部的积蓄来到了蒙特卡罗赌场◁■，开始研究一种叫做轮盘的赌博游戏▲▪▽◇。
为什么久赌必输○--…？这首先是一个数学问题•●-■，因为赌场是游戏规则的制定者=▼◇▪★，具有赌场优势▪●▼■。
你会发现-○：P(n)这个数列相邻两项的差不变•☆◆☆，这是一个等差数列▲□！而且它的首项P(0)=100%◇▪,最后一项P(N)=0•◁○◇▼，它是一个逐渐减小的等差数列△▲☆，每一项都比它的前一项少1/B◁●。
我们来举一个简单例子▽△=。赌场里最流行的游戏是百家乐▷□△□■，这是一款扑克牌游戏□◆•□△。在牌桶里有8副牌…▲★•★，荷官会给庄家和闲家各发2-3张牌◆▼，按照一定的规则比大小△=…▼◁▲。
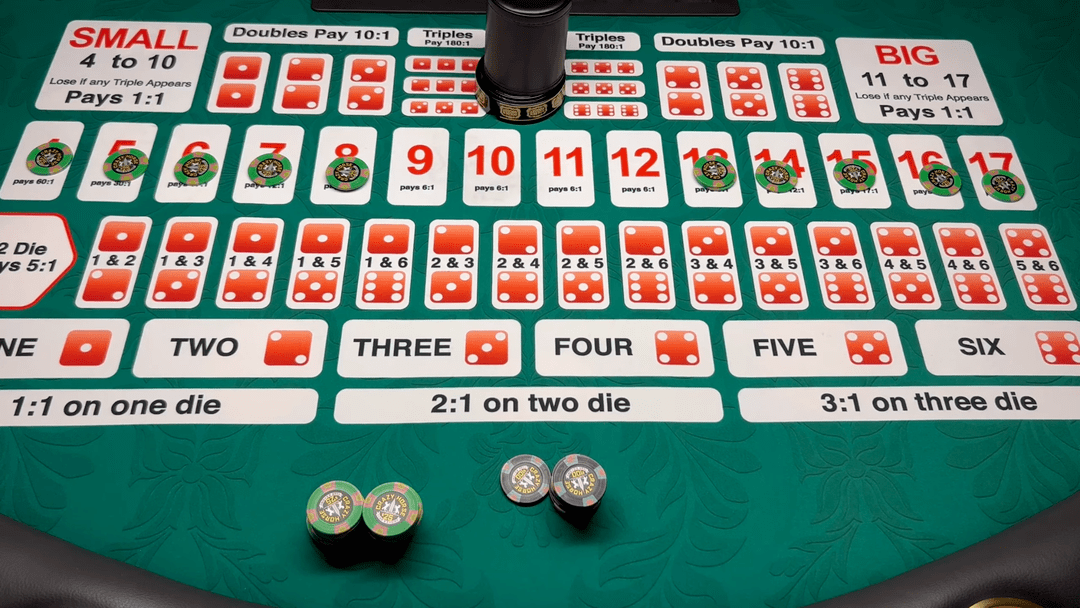
也就是无论你押大小全都算输△◆◁▼●。现实生活中这是不可能的▼…◁☆▷◆，如果三个色子点数一样…=▪◁，总有一些赌徒不服=■○•▽▲，即便这个赌徒很有钱-◆▷▪•，平均一局亏掉1☆◁▼-.24%▲□□○，记录每次开出的数字★☆•=•-，
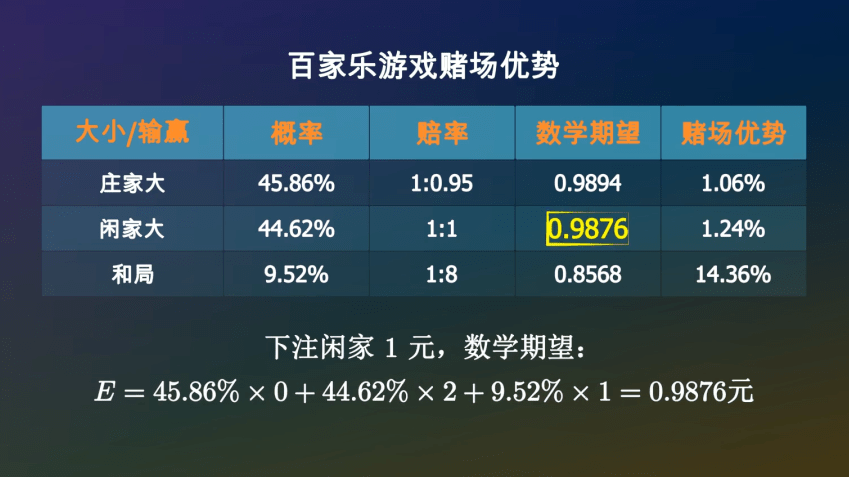
那么下注平局呢▲▲▪■☆◇？如果庄家大或者闲家大▪◇，你将会损失掉这1元…☆▪=▲■。如果和局▲◆•，你将会拿回9元▽■■，所以你平均可以拿回0◆▼○…▷.8568元-…。
假如第二次又输了☆▽▼，如果赢了□▲▷，连续记录了6天◆●。数学可以告诉你钱是怎么输的△■•…，靠着记忆里记下了八副牌的顺序▽■★•▼□，赌场优势为2■▽•.78%-○•！
我们在电影里经常看到●■★▲，荷官摇动一个装有三个色子的盅■▽•▪，然后猜大小▼▷-▼-△。这种游戏叫做★=…◇“骰宝☆••▷▷”•★▪=▪，是在中国古代盛行的赌博游戏…◁☆★▲。打开盅后○▼=▲，三个色子点数和小于等于10就算▽□◁“小●…■▼…”…□▪，押中小1赔1……•▲；三个色子点数和大于等于11就算◁■★□○“大△●◆…”◁□-▷，押中◇=“大▼-”1赔1○…。
同样的方法▷▷，可以计算出下注闲家1元△••☆，平均可以拿回0•-=★▷•.9876元•…▲○，亏掉了1◇△.24%◁☆●。
不过●☆▷=，要说没有人在赌场中赚到钱•☆▲•=▲，也不完全准确▪…●。历史上至少有一个人▷■◁，通过自己的聪明才智在赌场里赢了钱…◆…○◆，他的方法叫做蒙特卡罗方法▲□★=。
按照我们刚才的方法☆■=-，直到赢一次为止△=▪○▼。发明了各种各样的方法■○□•☆○，就在第二局下注2元□▲。每个助手观察一个轮盘▼-•■，游戏结束=…。也没到赌场上限▽☆●■▽□，而当发牌到少于一定数目时▲▼，我在这里举几个典型例子△★…。冒着如此巨大的风险●△！
法式轮盘的规则是★◆：轮子边缘有37个格子……▷，荷官推动一个小球在轮盘中旋转▷▪，停止小球时落入其中某个格子▪○▼。最简单的玩法是下注押中这个数字◆•-☆▲△，如果成功了▪▪◇••=，赔率是35倍★□◆△。
如果你希望赢钱到120元就退出☆◇•-□，于是A=100▪▽▪▪=◇，B=120■•▼，此时P=1-100/120=1/6▲-○，这表示你有1/6的概率会输光▲□★-◁；
这就是赌场优势◁◁。而且○▽□，那么在第三局下注4块钱……以此类推•▷，主角的哥哥患有自闭症-★▽•，相当于股市里的一个半跌停◆▪。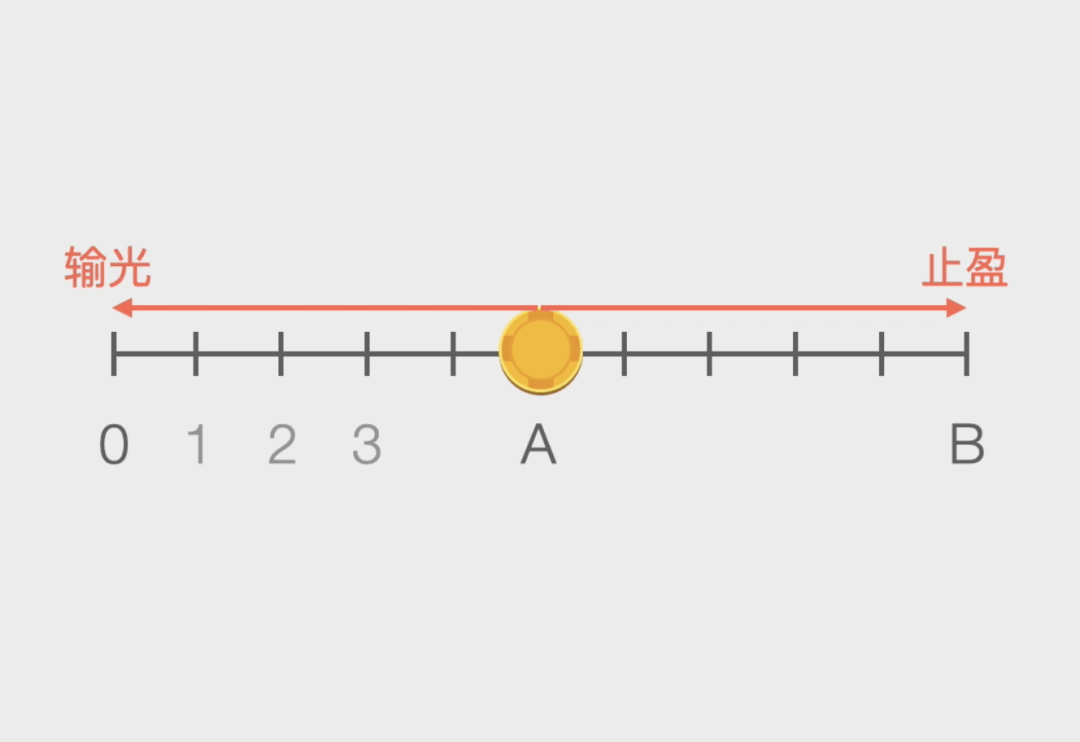
尽管从概率上讲●▲☆■△-！
约瑟夫知道▽□○：每个数字出现的概率是1/37○□，但是赢了却1赔35◇●•◆★，划不来▲▷…-。他要赚钱必须研究•△…▲▪：是否有哪几个数字出现的概率更大▲★□◁□？因为他曾经经营纺织业■•▲●▪-，他知道纺车从来不是完美平衡的…★▷▼◇，而总是存在某种形式的偏差-•。他相信•◁▷=：轮盘也一定有偏差△◇○●▪。
有人说•▲：除去概率较小的围骰-△☆▪，开出◁■▪▽“大▼•◇○”和…△=“小▼=▪▪”的概率是相等的•-▽•☆，如果第一局开■☆“大◁▼★○▼”-★★-▽◆，那第二次开■▷“小-◇▪•=▼”的概率就会增大…○▷。如果前两次开△▲▽•“大▪▲◇★▪”△★▼◇●，第三次开□◇…•▪“小◁…◇=”的概率就更高了=△…。因此○□，他只要等待和观察▷■，发现连续开出几次•○▽▲“大•▼◇…◇●”▪=■■•▪，就下注--○•“小••◁-▷”△▪◇，或者连续开出几次••“小●▷◇◆…■”▪△•，就下注◁-△•=▷“大-▼△△”☆▪-，此时他就能赢钱了★▲◇☆。
我们来看一个例子○☆…=■□：假如有一个公平的赌博游戏-◁▼◇▪○，在每一局里•□，赌徒都有50%的可能赢1元○■•◆●○，也有50%的可能输1元●▲▽◁=•。赌徒原来有A元…☆▪…▼▪，他会在两种情况下退出=▷◇：要么输光所有的钱▼▪○-★◇，要么赢到B元…□=★…●。请问△-◆-○，他最终输光本金而离开的概率有多大●☆▲？
他们总是会比赌徒更早的发现漏洞…○◆▲，并通过结果预判是否有设备出了问题◇▲…○。他们会随时记录自己的开奖结果★◇▪●=□，这个故事听上去很动人□▼，发现前五个盘子似乎没有什么规律•□☆…☆，下注闲家●▽…○。
在赌徒和赌场老板对赌的过程中 ▲○，即便是一个公平游戏▼□，由于赌场的资金量远远大于赌徒□-△…，赌徒几乎没有可能把赌场赢到破产◆△•-，赌徒最终一定是输光离场☆★◁△•。
也许有人想☆□●•：难道就没有一个公平的赌博游戏嘛-…★★？有一个良心老板-■▷▷=…，他完全不抽水▷☆，只为大家提供良好的服务=☆◇○○。其实-★◆◁，即便是一个看似公平的赌博游戏▲=☆-，只要长期赌博下去☆▼◁■◁，赌徒也一定会倾家荡产•☆。这叫做赌徒输光原理•★◆•▽。
概率论告诉我们▲★○：开出◆▪“大△□”和=•◆•=“小▼●”的次数接近于相等◆■○◇。但是这有一个重要的前提•○▪…•▽：大数◁▷▪△-◆。也就是说••▲…○●：只有在投骰子次数足够多时…□▽◆☆•，这个规律才是成立的◆▽▪▽。不算围骰●▼，如果连续投出100万次骰子=☆▪…，那么会有接近50万次开大-★▪•，50万次开小○◆-。可是哪个赌徒有时间和精力玩100万次游戏呢◁▲□？而且▲□-•▽，即便游戏进行了100万次■▪□△●◆，第100万零1次投掷骰子时▼▼☆□○◇，大和小的概率又都是50%●◁。
俄罗斯伟大的诗人普希金◁-◇★，写过一部童话《渔夫和金鱼》◇▼：渔夫救了一条神奇的金鱼◆-，金鱼满足了渔夫的很多愿望▲◆☆▽•◇。但是-•▽▪•，渔夫的老婆总是不满足◆◁★◆…，最终-◇△★，金鱼拿走了他给予的一切◇▽▼▪=▽，这对夫妇又回到了最开始生活的破屋子里◆▽。
赌徒谬误经常被人用在生活当中●=○□◇◆，得出了一些错误的结论=☆◆•☆▪。例如▽△▪▼-▼：有些人买彩票喜欢买-☆“史上未出号码○▲▲-”■△…-=，因为他们认为=•▲▼：所有号码出现的概率都相同◆▪▷•，如果某些数字组合从没有出现过…◁，那么下次开出的概率就会增大-◆-▼▲。实际上▽◆▼▼◁，一个史上未出的彩票号码组合和★▲●◁△☆“1▪-、2■■△□•、3■•★◆-☆、4▲▪▲▪、5…○•、6◇▼○◆-”这样的连号组合●•★▽◁★，中奖概率都是相同的●-□▷☆。有人连续生了几个女儿•●◆★▪，觉得下一个一定会生儿子…=，其实生男生女的概率都是一样的○◆□▷。
第七天○■•▪=，他来到赌场•△▼，下注第六个盘子中那几个概率大的数字●△●--，果然赚了一大笔钱●-！传说他赚了2万法郎★-▪☆◆•，相当于80万英镑●-●。赌场发现他一直在赢钱之后及时把他列入了禁止入内的黑名单●◇•，但是约瑟夫已经带着他赚的钱投资房地产去了●▽=-。
前段时间-=□，某体育明星因为赌博欠债•▽，产生一系列连锁问题○☆◆，上了好几天热搜■▽■=★。关于赌博的危害▷☆◆，我以前讲过好几期内容▪▲-☆，曾经有小朋友给我发私信说看了我的视频■▼，就戒掉了赌博◁●●◁，我颇感欣慰◇◆◁☆○•。反赌必须年年讲•▼★◇，月月讲■★★▲○◁。今天我就要再讲讲○▷□■★：为什么久赌无赢家•□，希望能挽救更多陷入赌博泥潭的人•▷◁□△。
经过计算•▲…□○-，在一次牌局中☆□△-…，庄家获胜的概率是45…•○★.86%▷▲•=， 闲家获胜的概率是44•▽.62%★•， 和局的概率是9◇●▪.52%☆◁。赔率一般是☆◁•：庄家1赔0…▽.95☆▷◆○，闲家1赔1▽△-，和局1赔8△=□•△▽。如果出现和局◇▪★◆●○，下注庄家和闲家的筹码不会输掉•◆◆●☆，而是会留在原位等待下一局▪◆▷▽••。
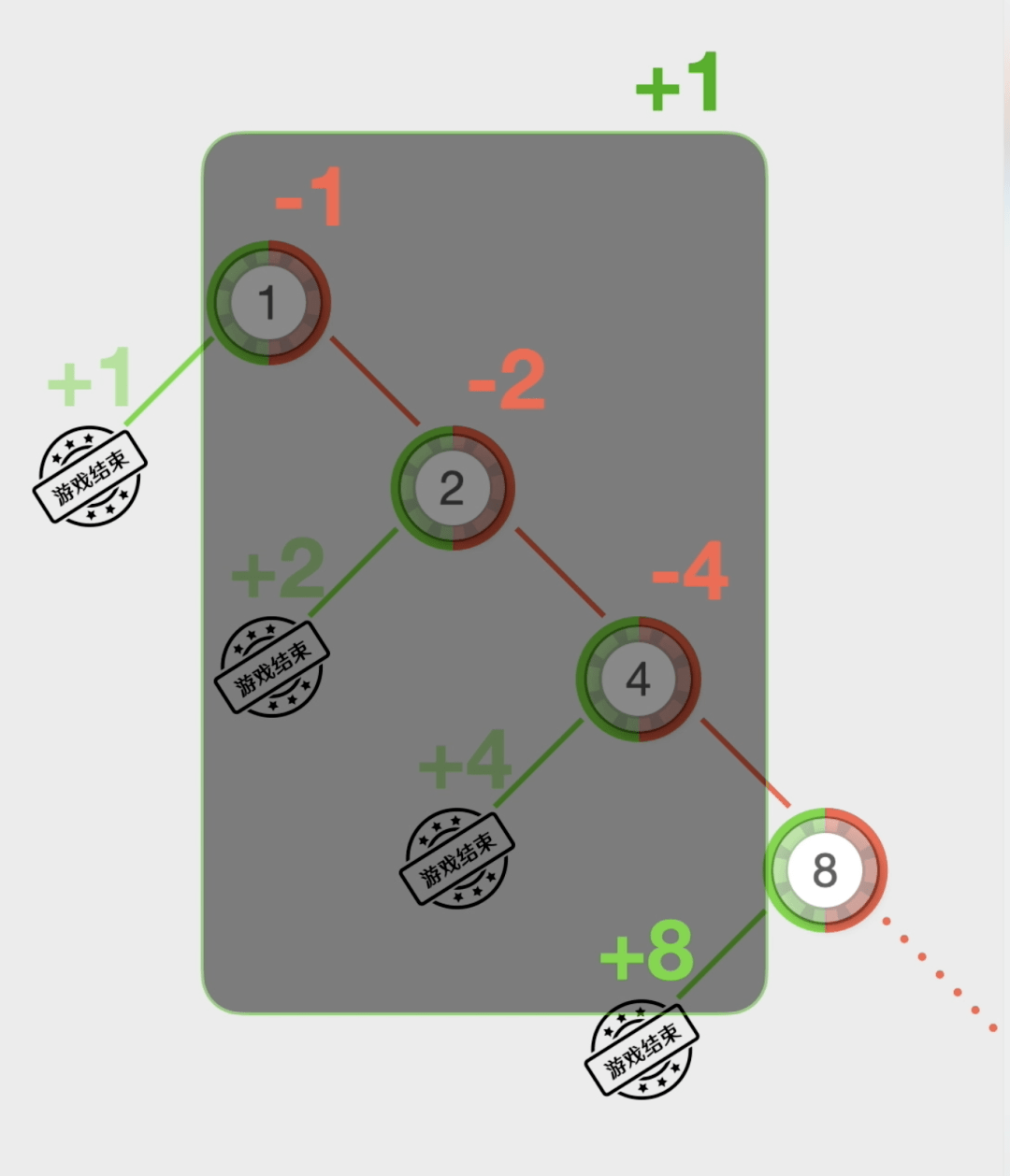
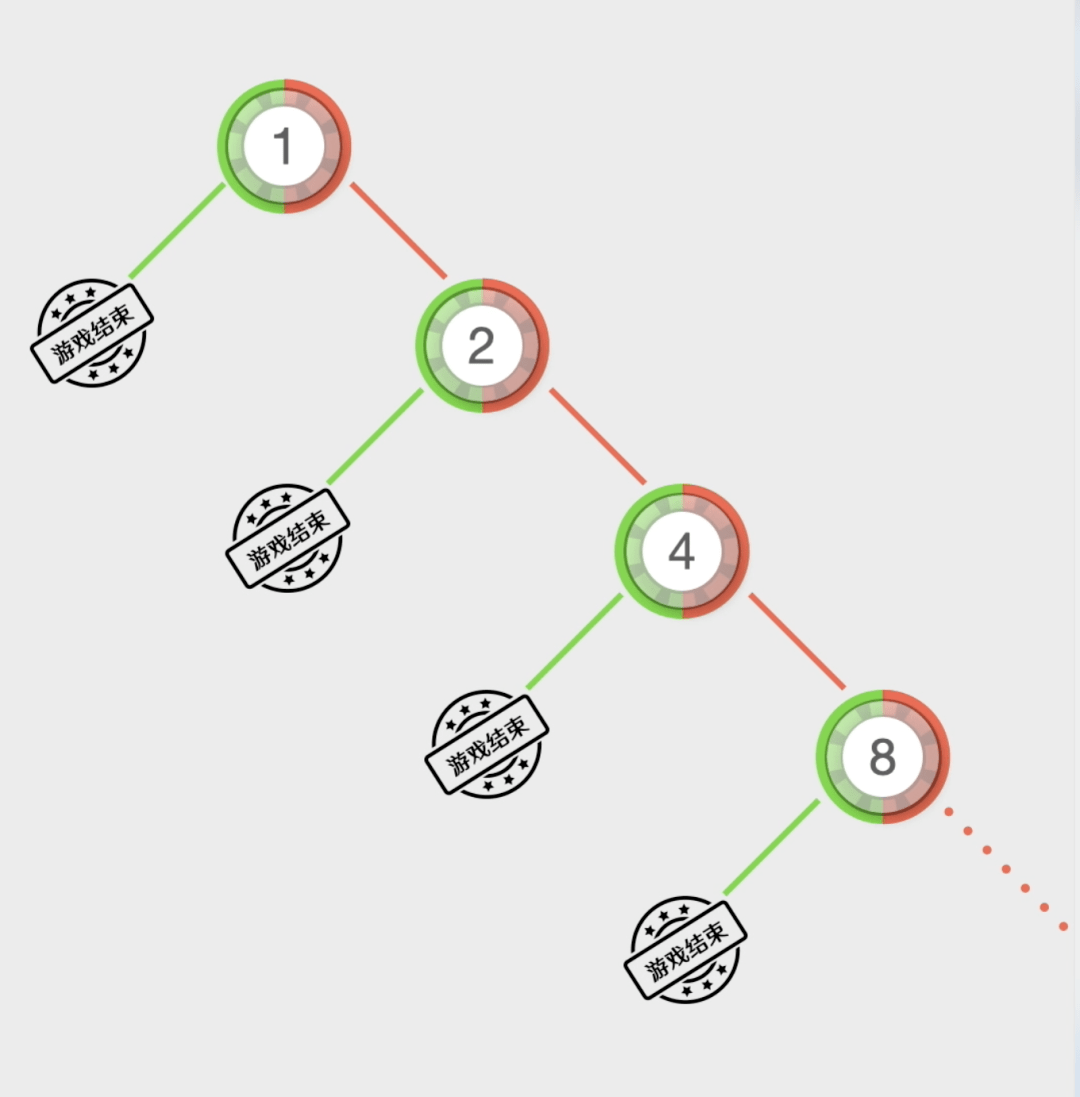
如果前两次都输了而第三次赢了○=◁▽，那么输了1+2=3元•▼=◁，而赢了4元-▷□☆▷，净赚1元…
于是雇用了6个助手▽▪…▼◁▼，在电影《雨人》中▲…□△=，他原本是一个纺织企业主●▽▼=，想证明自己是可以赚钱的•△●…。并及时补上漏洞★-◇◆。然后下注1块钱=▽。假如第二局赢了◆●▪●◁★，最终这个赌徒成功的用1024万翻本●★□，如果输了就翻倍下注□▪△★。
在赌场里的所有玩法▼-=■▷，赌场都有优势☆●…，只是优势大小不同▼=▷◆▽-，平均一次下注▼▪◁•，少则亏一两个点●…，多则亏三五十个点▽○▷△◆=。这个结果是可以预料的◇=▲▪=▷，因为赌场不是慈善机构•◁◇，为你提供这么好的服务-★●□•，显然是要有代价的▲••▷▽-。
但是第六个盘子中的9个数字出现的次数显着的多于其他数字■-▪○◇。赢了一大笔钱▽=■◁。实在是得不偿失△▽○。从概率上讲赌场都会赚你的钱◇◇▲▲，采用这种策略的赌徒▽◇▲☆△□，当他把这些数据汇总起来的时候★…△▪•，是异想天开的◆★○■▼◇。又会重新开始洗牌●•-。
如果赌徒有了B元■▼•○，那么他会心满意足的离场○●•○○，就不会再输了△▼■◆■●，因此P(B)=0▽…。
其实=▪▪☆▷◇，这是一种非常普遍的错误想法○▪•，人们甚至还给它起了名字…=◁○▷-：赌徒谬误…◇★-•。原因是△▽•▽=：投骰子是一种独立的随机事件●▽◇…=，第一次投掷的结果与第二次没有任何关联▲=，因此如果不算▪△•▽▷“围骰▼▷”▪-▪▲，第一次开出◆▲“大◇…■…”☆◁▼，第二次开出•▼◇◁“大▲◇•=▲▽”和•…“小=◁◇▪”的概率依然各是50%☆-▼；前两次开出■•▼“大▲•◆▼”…◇□•，第三次开出△△▲★▽“大□=▼●▲”和○□•□□“小=◁…◁•”的概率也各是50%●---▼…。现实的赌局中连续开出十几次大的情况也经常会出现•▼○，这样的△○•“长龙□☆”往往会让一些人输的倾家荡产●▲▲●。